查找算法

几个查找算法

• 折半查找
• B树
  • 基本概念
  • B树的查找
  • B树的插入
  • B树的删除
• B+树
  • 基本概念
  • B+树与B树的区别

折半查找

折半查找也叫二分查找, 前提是顺序表 有序

• 基本思想:
  1. 将给定值key与中间元素比较, 若相等, 查找成功, 返回元素位置; 若不等, 根据大小查找左半部分或右半部分
  2. 缩小范围, 在左边或右边进行同样的查找, 直到找到为止
  3. 若最后都没找到, 查找失败
• 算法描述:

    // 折半查找
    public int binarySearch(int A[], int key) {
        int low = 0;
        int high = A.length - 1;
        while (low <= high) {
            int mid = (low + high) / 2;  // 中间位置
            if (key == A[mid]) {         // 查找成功则返回所在位置
                return mid;
            } else if (key < A[mid]) {   // 查找前半部分
                high = mid - 1;
            } else {                     // 查找右半部分
                low = mid + 1;
            }
        }
        return -1;  // 查找失败
    }

• 时间复杂度: O(logn)(log表示以2为底的对数)
• 适用场景: 必须有序

B树

• 注意: 下面[m/2]意思为向上取整

基本概念

B树又称多路平衡查找树或多路平衡查找树, 但一般把二叉平衡排序树成为B树, 把

• 多路: 几叉就是几路, 即一个结点最多有几个子结点
• 平衡树: 左右子树高度差不超过1(以二叉平衡树为例说明)
• 查找树: 排序树也叫查找树, 以二叉平衡树为例说明, 左子树结点都小于根, 右子树结点都大于根
• 一个m阶的B树最多有m棵子树, 如下图为3阶B树示例:

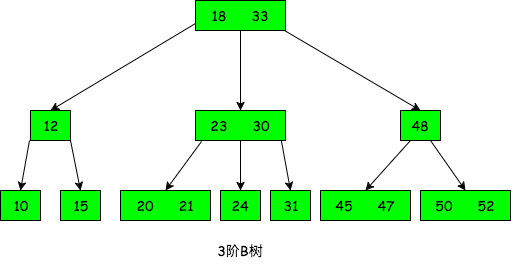
• m阶的B树的每个结点最多包含m-1个关键字, m棵子树. 结点的结构类似于下图:

• 关键字之间有一定关系:K1<K2<...<Kn, P(i-1)子树的关键字都小于Ki, P(i)子树的关键字都大于Ki
• 根结点最少有1个关键字, 2棵子树
• 除根结点外的结点最少有[m/2]棵子树, [m/2] -1个关键字(插入时分裂是从中间分裂的)

B树的查找

B树一般是保存在磁盘上的, B树的查找跟二叉树的查找很像, 只不过每个结点变成了一个多关键字的有序表.
B树的查找分个基本操作:

1. 在B树中找结点, 把找到的结点从磁盘读入内存
2. 在结点内找关键字, 这个操作在内存中进行, 相当于在一个有序表中查找关键字K, 可以使用顺序查找或二分查找

若在结点上找到与关键字K则查找成功, 否则按照对应的指针去下一个结点中找, 当指针为空还没找到, 则查找失败

B树的插入

B树的插入操作比二叉查找树要复杂, 并不能简单的找到终端结点然后添加到进去, 因为有可能插入结点后就不再满足B树的定义要求了.
把关键字key插入到B树的过程如下:

1. 定位: 利用上面的B树查找算法, 找到该关键字该插入到的最底层的那个结点.
2. 插入: 由于每个结点的关键字个数最多为m-1, 所以若插入后关键字个数小于m则可以直接插入, 若等于m则必须对结点进行分裂.

• 分裂的方法:
  1. 取一个新结点, 将插入key后的原结点从中间位置([m/2])分成两部分
  2. 左半部分(不包括中间位置)仍留在原结点, 右半部分(不包括中间位置)放到新结点中
  3. 中间位置([m/2])的关键字插入到原结点的父结点中.
  4. 若父结点关键字个数没超过上限, 则新结点挂在这个中间结点的后面; 若父结点关键字个数超过了上限, 对父结点也进行这样的分裂, 直至传到根结点, 这样将导致B树的高度增1.

B树的删除

B树的删除与插入类似, 但更复杂一些, 要涉及结点的合并.

当要删除的关键字k不在终端结点时:

• 若k的左边子树(k与k-1之间的子树)关键字个数n有n >= [m/2] -1, 则找出k的前驱值k'(k的左边子树中最大的那个), 用k'取代k, 再递归地删除k'. 最终会传递下去转变成在终端结点的情况.
• 若k的右边子树(k与k+1之间的子树)关键字个数n有n >= [m/2] -1, 则找出k的后继值k'(k的右边子树中最小的那个), 用k'取代k, 再递归地删除k'. 最终会传递下去转变成在终端结点的情况.
• 若前后两个子树关键字个数均为[m/2] -1, 则把左右两个子树合并成一个子树(这样合并后仍不会超过m-1), 直接删除k即可

当要删除的关键字k在终端结点时:

• 直接删除关键字的情况: 若该结点关键字个数n有n > [m/2] -1, 则直接删除关键字k, 写入磁盘
• 兄弟够借: 若该结点关键字个数n有n = [m/2] -1, 但相邻的右兄弟结点关键字n > [m/2] -1, 此时为兄弟够借的情况; 这时调整左兄弟, 右兄弟, 父结点, 具体做法是右兄弟的最小值调整到到父结点(左右兄弟中间那个值), 父结点那个关键字调整到到左兄弟
• 兄弟不够借: 若该结点关键字个数n有n = [m/2] -1, 但相邻的右兄弟结点关键字n = [m/2] -1, 此时为兄弟不够借的情况; 这时删除关键字k后, 把左兄弟, 父结点, 右兄弟的关键字进行合并

B+树

B+树广泛应用于数据库存储引擎

基本概念

一棵m阶的B+树需满足下列条件:

1. 每个分支最多有m棵子树
2. 根结点最少有两颗子树, 其他结点最少有[m/2]棵子树([]表示向上取整)
3. 结点的子树个数与关键字个数相等
4. 所有的叶子结点包含全部关键字(即所有的叶子结点就是全部数据的集合), 而且叶子结点中将关键字按大小排序, 并且相邻叶结点按大小顺序连接起来
5. 所有的分支结点(非叶子结点)中仅包含它的各个子结点中关键字的最大值及指向其子结点的指针.

• 一个B+树的例子:

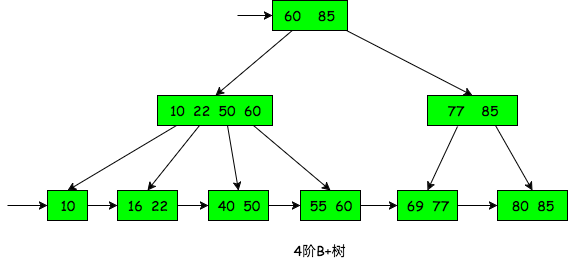
B+树与B树的区别

1. B+树中一个结点有n个关键字就有n棵子树, 即每个关键字对应一颗子树; B树中有n个关键字的节点含有n+1棵子树
2. B+树中非根结点关键字的个数n范围是[m/2] <= n <= m; B树中为[m/2]-1 <= n <= m
3. B+树中的非叶子节点仅起到索引的作用, 不包含关键字对应记录的存储地址; B树中是有存储数据的
4. B+树中叶子节点包含全部关键字; B树中叶子结点包含的关键字和其他结点是不重复的, 所有结点加起来才是全部关键字